|
前面我们从代数角度出发讨论了控制系统稳定性的定义和劳斯-赫尔维茨稳定判据。本节介绍判别系统稳定性的另一种判据――奈奎斯特稳定判据。该判据是根据开环频率特性来判定闭环系统的稳定性。同时,它还能反映系统的相对稳定的程度,对于不稳定的系统,判据与劳斯稳定判据一样,还能确切回答闭环系统有多少个不稳定的特征根。
对于图5-34所示的反馈控制系统,闭环传递函数为:
其特征方程式为
令
将式(5-40)代入式(5-39)得
式中, 、 、 、…、 、…、 是 是 的零点,也是闭环特征方程式的根; 的零点,也是闭环特征方程式的根; 、 、  、…、 是 、…、 是 的极点,也是开环传递函数的极点。因此根据前述闭环系统稳定的充分必要条件,要使闭环系统稳定,特征函数 的极点,也是开环传递函数的极点。因此根据前述闭环系统稳定的充分必要条件,要使闭环系统稳定,特征函数 的全部零点都必须位于s平面的左半平面上。 的全部零点都必须位于s平面的左半平面上。
5.4.1 辐角原理
由于 是s的有理分式,则由复变函数的理论知道, 是s的有理分式,则由复变函数的理论知道, 除了在s平面上的有限个奇点外,它总是解析的,即为单值、连续的正则函数。因而对于s平面上的每一点,在 除了在s平面上的有限个奇点外,它总是解析的,即为单值、连续的正则函数。因而对于s平面上的每一点,在 平面上必有唯一的一个映射点与之相对应。同理,对s平面上任意一条不通过 平面上必有唯一的一个映射点与之相对应。同理,对s平面上任意一条不通过 的极点和零点的闭合曲线 的极点和零点的闭合曲线 ,在 ,在 平面上必有唯一的一条闭合曲线 平面上必有唯一的一条闭合曲线  与之相对应,如图5-35所示。若s平面上的闭合曲线 与之相对应,如图5-35所示。若s平面上的闭合曲线 按顺时针方向运动,则其在 按顺时针方向运动,则其在 平面上的映射曲线 平面上的映射曲线 的运动方向可能是顺时针,也可能是逆时针,它完全取决于复变函数 的运动方向可能是顺时针,也可能是逆时针,它完全取决于复变函数 本身的特性。在此我们感兴趣的不是映射曲线 本身的特性。在此我们感兴趣的不是映射曲线 的具体形状,而是它是否包围 的具体形状,而是它是否包围 平面的坐标原点以及围绕原点的方向和圈数,因为它与系统的稳定性有着密切的关系。 平面的坐标原点以及围绕原点的方向和圈数,因为它与系统的稳定性有着密切的关系。
| 图5-35 s平面上封闭曲线及其在F(s)平面上的映射线 |
图5-35 s平面上封闭曲线及其在F(s)平面上的映射线
由式(5-41)可知,复变函数 的相角为 的相角为
假设s平面上的闭合曲线 以顺时针方向围绕 以顺时针方向围绕 的一个零点- 的一个零点- , , 的其余零点和极点均位于闭合曲线 的其余零点和极点均位于闭合曲线 之外。当点s沿着闭合曲线 之外。当点s沿着闭合曲线  走了一周时,向量 走了一周时,向量 的相角变化了 的相角变化了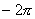 ,其余各向量的相角变化都为 ,其余各向量的相角变化都为 。这表示在 。这表示在 平面上的映射曲线按顺时针方向围绕着坐标原点旋转一周,如图5-36所示。由此推论,若s平面上的闭合曲线 平面上的映射曲线按顺时针方向围绕着坐标原点旋转一周,如图5-36所示。由此推论,若s平面上的闭合曲线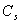 以顺时针方向包围 以顺时针方向包围 的z个零点,则在 的z个零点,则在 平面上的映射曲线 平面上的映射曲线 将按顺时针方向围绕着坐标原点旋转z周。 将按顺时针方向围绕着坐标原点旋转z周。
如果s平面上的闭合曲线 按顺时针方向围绕着 按顺时针方向围绕着 的一个极点 的一个极点 旋转一周,则向量 旋转一周,则向量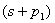 的相角变化了 的相角变化了 。由式(5-42)可知, 。由式(5-42)可知, 的相角变化了 的相角变化了 。这表示 。这表示 平面上的映射曲线 平面上的映射曲线 按逆时针方向围绕其坐标原点一周。由此推广到一般,若s平面上的闭合曲线 按逆时针方向围绕其坐标原点一周。由此推广到一般,若s平面上的闭合曲线 按顺时针方向围绕着 按顺时针方向围绕着 的p个极点旋转一周,则其在 的p个极点旋转一周,则其在 平面上的映射曲线 平面上的映射曲线 按逆时针方向围绕着坐标原点旋转p周。 按逆时针方向围绕着坐标原点旋转p周。
综上所述,可得到如下的辐角原理。
辐角原理 设除了有限个奇点外, 是一个解析函数。如果s平面上的闭合曲线 是一个解析函数。如果s平面上的闭合曲线 以顺时针方向包围了 以顺时针方向包围了 的Z个零点和P个极点,且此曲线不通过 的Z个零点和P个极点,且此曲线不通过 的任何极点和零点,则其在 的任何极点和零点,则其在 平面上的映射曲线 将围绕着坐标原点旋转N周,其中 平面上的映射曲线 将围绕着坐标原点旋转N周,其中 。若 。若 ,表示曲线 ,表示曲线 以顺时针方向围绕;若 以顺时针方向围绕;若 ,则表示曲线 ,则表示曲线 以逆时针方向围绕。 以逆时针方向围绕。
5.4.2 奈奎斯特稳定判据
如果闭环系统是稳定的,则其特征方程式的根,即 所有的零点均位于s的左半平面。为了判别系统的稳定性,检验 所有的零点均位于s的左半平面。为了判别系统的稳定性,检验 是否有零点在s的右半平面上即可。为此,在s平面上所取的闭合曲线 是否有零点在s的右半平面上即可。为此,在s平面上所取的闭合曲线 应包含s的整个右半平面,如图5-37所示。这样,如果 应包含s的整个右半平面,如图5-37所示。这样,如果 有零点或极点在s的右半平面上,则它们必被此曲线所包围。这一闭合曲线称为奈奎斯特轨线,它是由 有零点或极点在s的右半平面上,则它们必被此曲线所包围。这一闭合曲线称为奈奎斯特轨线,它是由 轴表示的 轴表示的 部分和半径为无穷大的半圆 部分和半径为无穷大的半圆 部分组成。即s按顺时针方向沿着 部分组成。即s按顺时针方向沿着 由 由 运动到 运动到 ,尔后沿着半径为无穷大的半圆 ,尔后沿着半径为无穷大的半圆 由 由 运动到 运动到 ,其中 ,其中 。 。
由于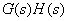 中的 中的 ,当s沿着奈氏轨线 ,当s沿着奈氏轨线 运动时,有 运动时,有
 =常数 =常数
这说明当s沿着半径为无穷大的半圆变化时,函数 始终是一常数。由此, 始终是一常数。由此, 平面上的映射曲线 平面上的映射曲线 是否包围坐标原点,只取决于奈氏轨线中 是否包围坐标原点,只取决于奈氏轨线中 部分的映射,即由 部分的映射,即由 轴的映射曲线来表征。 轴的映射曲线来表征。
设在  轴上不存在 轴上不存在 的极点和零点,则当s沿着 的极点和零点,则当s沿着 轴由 轴由  运动到 运动到 时,在 时,在 平面上的映射曲线 平面上的映射曲线 为 为
设闭合曲线 以顺时针方向包围了 以顺时针方向包围了 的z个零点和p个极点,由辐角原理可知,在 的z个零点和p个极点,由辐角原理可知,在 平面上的映射曲线 平面上的映射曲线 将按顺时针方向围绕着坐标原点旋转N周,其中 将按顺时针方向围绕着坐标原点旋转N周,其中
由于
因而映射曲线 对其坐标原点的围绕相当于开环频率特征曲线 对其坐标原点的围绕相当于开环频率特征曲线 对GH平面上的(-1,j0)点的围绕,图5-38示出了奈氏曲线映射在这两个平面上的位置。 对GH平面上的(-1,j0)点的围绕,图5-38示出了奈氏曲线映射在这两个平面上的位置。
通过上述分析可知,闭环系统的稳定性可通过其开环频率响应 曲线对(-1,j0)点的包围与否来判别,这就是下述的奈奎斯特稳定判据。 曲线对(-1,j0)点的包围与否来判别,这就是下述的奈奎斯特稳定判据。
奈奎斯特稳定判据:
(1) 如果开环系统是稳定的,即P=0,则闭环系统稳定的充要条件是 曲线不包围(-1,j0)点。 曲线不包围(-1,j0)点。
(2) 如果开环系统不稳定,且已知有P个开环极点在s的右半平面,则闭环系统稳定的充要条件是 曲线按逆时针方向围绕(-1,j0)点旋转P周。 曲线按逆时针方向围绕(-1,j0)点旋转P周。
综上,应用奈氏判据判别闭环系统的稳定性的具体步骤为:
(1)首先要确定开环系统是否稳定,若不稳定,则P为多少?
(2)作出奈氏曲线 。具体作图时可先画出 。具体作图时可先画出 从0到 从0到 的一段曲线,然后以实轴为对称轴,画出 的一段曲线,然后以实轴为对称轴,画出 从0到 从0到 的另一段曲线,从而得到完整的奈氏曲线。 的另一段曲线,从而得到完整的奈氏曲线。
(3)计算奈氏曲线 对点(-1,j0)按顺时针方向的包围圈数N。 对点(-1,j0)按顺时针方向的包围圈数N。
(4)根据辐角原理确定Z是否为零。如果Z=0,表示.闭环系统稳定;反之, ,表示该闭环系统不稳定。Z的数值反映了闭环特征方程式的根在s右半平面上的个数。 ,表示该闭环系统不稳定。Z的数值反映了闭环特征方程式的根在s右半平面上的个数。
例 5-5 试用奈氏判据判别闭环系统的稳定性。
系统的开环传递函数为
试用奈氏判据判别闭环系统的稳定性。
解:当ω由 变化时, 变化时, 曲线如图5-39所示。因为 曲线如图5-39所示。因为 的开环极点为-0.5,-1,-2,在s的右半平面上没有任何极点,即P=0,由图5-39可知,由于奈氏曲线不包围(-1,j0)这点,因此N=0,则Z=N+P=0。这表示该闭环系统是稳定的。 的开环极点为-0.5,-1,-2,在s的右半平面上没有任何极点,即P=0,由图5-39可知,由于奈氏曲线不包围(-1,j0)这点,因此N=0,则Z=N+P=0。这表示该闭环系统是稳定的。
5.4.3 奈奎斯特稳定性判据的进一步说明
1、开环极点位于虚轴的情况
如果 在虚轴上存在极点,那么就不能直接用图5-37所示的奈氏轨线 在虚轴上存在极点,那么就不能直接用图5-37所示的奈氏轨线 ,因为辐角原理只适用于奈氏轨线 ,因为辐角原理只适用于奈氏轨线 不通过 不通过 的奇点。为此,可对图5-37所示的奈氏轨线作些修改,使其沿着半径为 的奇点。为此,可对图5-37所示的奈氏轨线作些修改,使其沿着半径为 的半圆绕过虚轴上的所有极点。假设开环系统在坐标原点处有其极点,则对应的奈氏途径要修改为如图5-40所示。比较图5-40与图5-37可以发现,它们的区别在于图5-40中多了一个半径为无穷小的半圆 的半圆绕过虚轴上的所有极点。假设开环系统在坐标原点处有其极点,则对应的奈氏途径要修改为如图5-40所示。比较图5-40与图5-37可以发现,它们的区别在于图5-40中多了一个半径为无穷小的半圆 部分,其余两者完全相同。因此,只需要研究图5-40中的 部分,其余两者完全相同。因此,只需要研究图5-40中的 部分在GH平面上的映射。 部分在GH平面上的映射。
设系统的开环传递函数
在 部分上,令 部分上,令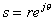 ,其中 ,其中 ,代入上式得 ,代入上式得
当s按逆时针方向沿着 由点a移动到c时,由式(5-46)可求得其在GH平面上的映射曲线: 由点a移动到c时,由式(5-46)可求得其在GH平面上的映射曲线:
对于 的I型系统, 的I型系统, 部分在GH平面上的映射曲线为一个半径为无穷大的半圆,如图5-41a所示。图中点 部分在GH平面上的映射曲线为一个半径为无穷大的半圆,如图5-41a所示。图中点 、 、 和 和  分别为 分别为 半圆上点a、b和c的映射点。 半圆上点a、b和c的映射点。
对于 的Ⅱ型系统, 的Ⅱ型系统, 部分在GH平面上的映射曲线是一个半径为无穷大的半圆,如图5-41b所示。 部分在GH平面上的映射曲线是一个半径为无穷大的半圆,如图5-41b所示。
把上述 部分在GH平面上的映射曲线和 部分在GH平面上的映射曲线和 的奈氏曲线在 的奈氏曲线在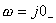 和 和 处相连接,就组成了一条封闭曲线。此时,又可应用奈奎斯特稳定判据了。 处相连接,就组成了一条封闭曲线。此时,又可应用奈奎斯特稳定判据了。
例5-6 试判别该系统的稳定性。
反馈控制系统开环传函数为
试判别该系统的稳定性。
解:由于该系统为I型系统,它在坐标原点处有一个开环极点,因而在s上所取的奈氏轨线应如图5-40所示。该图的 部分在GH平面上的映射曲线为一半径为无穷大的半圆,若将它与图5-42的奈氏曲线 部分在GH平面上的映射曲线为一半径为无穷大的半圆,若将它与图5-42的奈氏曲线 相连接,则有N=2,而系统的P=0,因而Z=2,即闭环系统是不稳定的,且有两个闭环极点位于s的右半平面。 相连接,则有N=2,而系统的P=0,因而Z=2,即闭环系统是不稳定的,且有两个闭环极点位于s的右半平面。
例5-7 试分析时间常数的相对大小对系统稳定性的影响并画出它们所对应的奈氏图。
已知系统的开环传递函数为
试分析时间常数 和 和 的相对大小对系统稳定性的影响,并画出它们所对应的奈氏图。 的相对大小对系统稳定性的影响,并画出它们所对应的奈氏图。
解 由开环传递函数得
根据以上两式,作出在 , , 和 和 三种情况下的 三种情况下的 曲线,如图5-43所示。当 时, 曲线不包围(-1,j0)点,因而闭环系统稳定的。当 曲线,如图5-43所示。当 时, 曲线不包围(-1,j0)点,因而闭环系统稳定的。当 时, 时, 曲线通过(-1,j0)点,说明闭环极点位于 曲线通过(-1,j0)点,说明闭环极点位于 轴上,相应的系统为不稳定的。当 轴上,相应的系统为不稳定的。当 时, 时, 曲线以顺时针方向包围(-1,j0)点旋转两周,这意味着有两个闭环极点位于s右半平面上,该闭环系统是不稳定的。 曲线以顺时针方向包围(-1,j0)点旋转两周,这意味着有两个闭环极点位于s右半平面上,该闭环系统是不稳定的。
2、利用奈氏判据确定系统的参数稳定范围
如果系统中的某个参数或若干个参数是可以变化的,为使系统稳定,可利用奈氏判据来确定系统的参数稳定范围,即根据奈氏曲线是否通过(-1,j0)点的条件来选定参数。下面以例说明之。
例5-8 试用奈氏判据确定该闭环系统稳定的K值范围。
已知一单位反馈系统的开环传递函数为
试用奈氏判据确定该闭环系统稳定的K值范围。
解 该系统是一个非最相位系统,其开环系统幅频和相频特性的表达式分别为
和惯性环节一样,它的奈氏图也是一个圆,如图5-44所示。由于系统的P=1,当ω由 变化时, 变化时,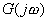 曲线如按逆时针方向围绕(-1,j0)点旋转一周,即N=-1,则Z=1-1=0,表示闭环系统是稳定的。由图5-44可见,系统稳定的条件是K>1。 曲线如按逆时针方向围绕(-1,j0)点旋转一周,即N=-1,则Z=1-1=0,表示闭环系统是稳定的。由图5-44可见,系统稳定的条件是K>1。
3、具有时滞环节的稳定性分析
由于时滞系统的开环传递函数中有着 的环节,其闭环特征方程为一超越方程,因而劳斯稳定判据就不适用了。但是,奈氏稳定判据却能较方便地用于对这类系统稳定性的判别。 的环节,其闭环特征方程为一超越方程,因而劳斯稳定判据就不适用了。但是,奈氏稳定判据却能较方便地用于对这类系统稳定性的判别。
设含有时滞环节的开环系统的传递如下:
式中,  为时滞时间常数。将上式改写成: 为时滞时间常数。将上式改写成:
其中
不含时滞环节的传递函数。相应地,开环系统的幅频特性和相频特性为:
上式表明,当 时,相对于 时,相对于 , , 的幅值没有变化,而相角则在每个 的幅值没有变化,而相角则在每个 上顺时针多转动了 上顺时针多转动了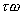 。 。
由于实际的控制系统中, ,因此当 ,因此当 时, 时, 的模趋于零,因而 的模趋于零,因而 随 随 以螺旋形趋于原点,并且与GH平面的负半轴相交无穷点,如图5-45。因此为使系统稳定,奈氏曲线与负实轴相交点必须位于(-1,j0)的左边。 以螺旋形趋于原点,并且与GH平面的负半轴相交无穷点,如图5-45。因此为使系统稳定,奈氏曲线与负实轴相交点必须位于(-1,j0)的左边。
例5-9 试分析滞后时间 对系统稳定性的影响。
设一时滞控制系统如图5-46所示。已知图中的  ,试分析滞后时间 ,试分析滞后时间 对系统稳定性的影响。 对系统稳定性的影响。
解 系统的开环传递函数为
取 值分别为0,2,4,图5-47示出了式(5-51)在不同 值分别为0,2,4,图5-47示出了式(5-51)在不同  值时的奈氏曲线。由图可见,当滞后时间 值时的奈氏曲线。由图可见,当滞后时间 为零时,系统相当于无时滞环节, 为零时,系统相当于无时滞环节, 不包围(-1,j0),所以闭环系统是稳定的;当 不包围(-1,j0),所以闭环系统是稳定的;当 =2时, =2时, 刚好经过(-1,j0),系统处于临界稳定状态;当 刚好经过(-1,j0),系统处于临界稳定状态;当 =4时, =4时, 包围(-1,j0)点,所以闭环系统是不稳定的。可见,时滞时间的增大,对控制系统的稳定和性能都是极为不利的。 包围(-1,j0)点,所以闭环系统是不稳定的。可见,时滞时间的增大,对控制系统的稳定和性能都是极为不利的。
5.4.4 奈氏稳定判据在对数坐标图上的应用
与奈氏图的绘制相比,开环对数频率特性的绘制更为简单、方便,因而研究开环对数频率特性形式的奈氏稳定判据是有实际意义的。注意到开环系统的奈氏图与相应的对数坐标图之间有着下列的对应关系:
1)GH平面上单位圆的圆周与对数坐标图上的0dB线相对应,单位圆的外部对应于 ,单位圆的内部对应于 ,单位圆的内部对应于 。 。
2)GH平面上的负实轴与对数坐标图上的 线相对应。 线相对应。
如果 曲线以逆时针方向包围(-1,j0)点一周,则此曲线必然由上向下穿越负实轴的 曲线以逆时针方向包围(-1,j0)点一周,则此曲线必然由上向下穿越负实轴的 线段一次。由于这种穿越使相角增大,故称为正穿越,其次数用 线段一次。由于这种穿越使相角增大,故称为正穿越,其次数用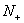 表示。反这,若 表示。反这,若 曲线按顺时针方向包围(-1,j0)点一周,则此曲线将由下向上穿越负实轴的 曲线按顺时针方向包围(-1,j0)点一周,则此曲线将由下向上穿越负实轴的 线段一次。由于这种穿越使相角减小,故称为负穿越,其次数用 线段一次。由于这种穿越使相角减小,故称为负穿越,其次数用 表示。图5-48a所示的为正负穿越数各一次的图形。显然,对应于图5-48a上的正负穿越在伯德图上表现为:在 表示。图5-48a所示的为正负穿越数各一次的图形。显然,对应于图5-48a上的正负穿越在伯德图上表现为:在 的频域内,当 的频域内,当 增加时,相频曲线 增加时,相频曲线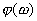 由下而上(负穿越)和由上而下(正穿越)穿过 由下而上(负穿越)和由上而下(正穿越)穿过 线各一次,如图5-48b所示。 线各一次,如图5-48b所示。
不难看出,在极坐标图上 曲线对于(-1,j0)点的包围圈数N与其相频特性曲线 曲线对于(-1,j0)点的包围圈数N与其相频特性曲线 在对数坐标图上的负,正穿越数之差相等。即有 在对数坐标图上的负,正穿越数之差相等。即有
式中 , 为在 , 为在  频率范围内 频率范围内 的负穿越数; 的负穿越数; 为在 为在 频率范围内 频率范围内 的正穿越数。这样,式(5-44)便可改写为 的正穿越数。这样,式(5-44)便可改写为
应用上式,就可得到对数频率特性形式的奈奎斯特判据:闭环系统稳定的充要条件是,当 变化时,在 变化时,在 频率范围内,相率特性 频率范围内,相率特性 穿越 穿越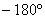 线的次数(正、负穿越数之差)为 线的次数(正、负穿越数之差)为 。 。
在使用对数频率特性的奈氏稳定判据时,应注意如下两点:
(1) 判据中的频率范围是 ,而非如前述的 ,而非如前述的  ; ;
(2) 若P为奇数,则意味着开环系统并未产生真正的穿越,即相频特性的起点在负半轴 | 





































