[资料分享] MSP430FR2311 中 UART 通讯的累积误差分析计算和时钟频率优选

fish001 2019-4-9 19:49 楼主

在UART通讯设计中，工程师会根据系统需要先选定合适的波特率（Baud Rate），然后选择合适的时钟源频率，以使UART传输数据时的累积误差最小，数据的误码率最低。本文以MSP430FR2311为例，对UART数据传输过程中发送端累积误差和接收端累积误差进行了详细的分析和计算。根据计算结果，工程师可以优选出时钟源频率，提高UART数据传输系统的可靠性。

在附录1的文章中，对MSP430FR2311的UART模块寄存器配置的分析和计算有了详细介绍，这里不再赘述。BRCLK是时钟源频率，BITCLK是波特率。当BRCLK是BITCLK的整数倍，即BRCLK/BITCLK=N，由于每个数据bit中含有N个BRCLK，和理想值完全相同，所以每个数据bit不存在时长误差，因此在数据传输过程中也不存在累积误差。但是大部分情况下BRCLK不是BITCLK的整数倍，由于在数据传输过程中，每个数据bit时长都是BRCLK的整数倍，这样在每个数据bit中就存在时长误差，因此在数据传输过程中也就存在累积误差。

以下分4部分进行累积误差的分析和计算：低频波特率的发射端累积误差，高频波特率的发射端累积误差，低频波特率的接收端累积误差，高频波特率的接收端累积误差。

低频波特率的发射端累积误差

以时钟源频率BRCLK 32768Hz，波特率BITCLK 2400Hz为例，32768/2400=13.6533，所以UCOS16=0，UCBRx=13，UCBRSx=0xB6.

如图1所示，在每个数据bit的发送结束时刻，实际发送时长和理想发送时长存在误差。

对于Start bit，理想时长13.65BRCLK，实际时长14BRCLK，误差时长为13.65BRCLK-14BRCLK=-0.35BRCLK。

对于LSB bit，理想时长13.65BRCLK，实际时长13BRCLK，误差时长为13.65BRCLK-13BRCLK=0.65BRCLK，累积误差时长为-0.35BRCLK+0.65BRCLK=0.30BRCLK。

对于Bit1，理想时长13.65BRCLK，实际时长14BRCLK，误差时长为13.65BRCLK-14BRCLK=-0.35BRCLK，累积误差时长为0.30BRCLK-0.35BRCLK=-0.05BRCLK。

后续bit位的误差和累积误差以此类推。

图1低频波特率的发射端累积误差示意图

以下是低频波特率的发射端累积误差的公式推导。

t_bits_ideal_TX为发送端理想累积数据时长。

t_bits_ideal_TX = (i+1)/BITCLK (1)

t_bit_period_TX为发送端实际每个数据bit时长。每个数据的BRCLK个数等于UCBRx值和UCBRSx的对应调制值UCBRSx.m之和。

t_bit_period_TX = (UCBRx +UCBRSx.m)/BRCLK (2)

t_bits_TX为发送端实际发送的累积数据时长。

t_bits_TX[0] = t_bit_period_TX[0] (3)

t_bits_TX = t_bits_TX[i-1] + t_bit_period_TX, 其中i≠0 (4)

定义Error_TX为实际累积数据时长与理想累积数据时长的差值，相对于理想数据bit时长的百分比，单位为%

Error_TX=( t_bits_ideal_TX- t_bits_TX)*BITCLK*100 (5)

表1为带入例程中数据的Error_TX的计算结果。

从表1中可以看到，最大正Error_TX为3.91%，最小负Error_TX为-3.12%.

表1 Error_TX

高频波特率的发射端累积误差
以时钟源频率BRCLK 4000000Hz，波特率BITCLK 57600为例，4000000/57600=69.4444，所以UCOS16=1，UCBRx=4，UCBRFx=5，UCBRSx=0x55.
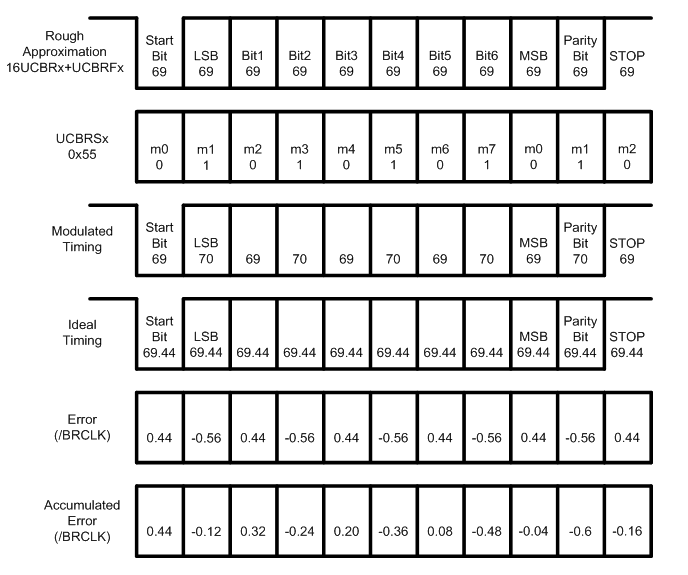
如图2所示，在每个数据bit的发送结束时刻，实际发送时长和理想发送时长存在误差。
对于Start bit，理想时长69.44BRCLK，实际时长69BRCLK，误差时长为69.44BRCLK-69BRCLK=0.44BRCLK。
对于LSB bit，理想时长69.44BRCLK，实际时长70BRCLK，误差时长为69.44BRCLK-70BRCLK=-0.56BRCLK，累积误差时长为0.44BRCLK-0.56BRCLK=-0.12BRCLK。
对于Bit1，理想时长69.44BRCLK，实际时长69BRCLK，误差时长为69.44BRCLK-69BRCLK=0.44BRCLK，累积误差时长为-0.12BRCLK+0.44BRCLK=0.32BRCLK。
后续bit位的误差和累积误差以此类推。

图2高频波特率的发射端累积误差示意图
以下是高频波特率的发射端累积误差的公式推导。
t_bits_ideal_TX为发射端理想累积数据时长。
t_bits_ideal_TX = (i+1)/BITCLK                                                                                                                            (6)
t_bit_period_TX为发射端实际每个数据bit时长。每个数据的BRCLK个数等于16*UCBRx+UCBRFx值和UCBRSx的对应调制值UCBRSx.m之和。
t_bit_period_TX = (16*UCBRx+UCBRFx +UCBRSx.m)/BRCLK                                                                      (7)
t_bits_TX为发射端实际发送的累积数据时长。
t_bits_TX[0] = t_bit_period_TX[0]                                                                                                                         (8)
t_bits_TX = t_bits_TX[i-1] + t_bit_period_TX, 其中i≠0                                                                            (9)
定义Error_TX为实际累积数据时长与理想累积数据时长的差值，相对于理想数据bit时长的百分比，单位为%
Error_TX=( t_bits_ideal_TX- T_bits_TX)*BITCLK*100                                                                            (10)

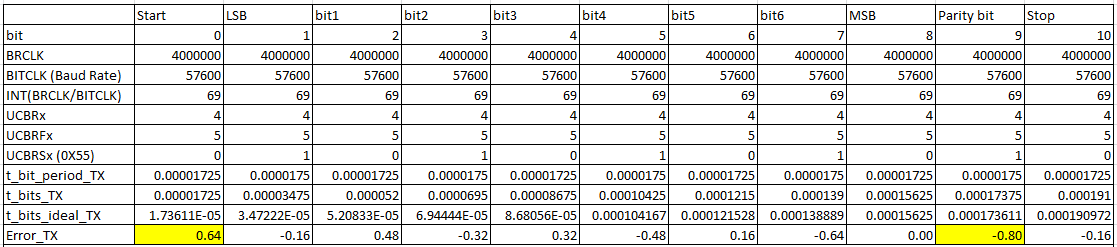
表2为带入例程中数据的Error_TX的计算结果。
从表2中可以看到，最大正Error_TX为0.64%，最小负Error_TX为-0.80%.
表2 Error_TX

低频波特率的接收端累积误差
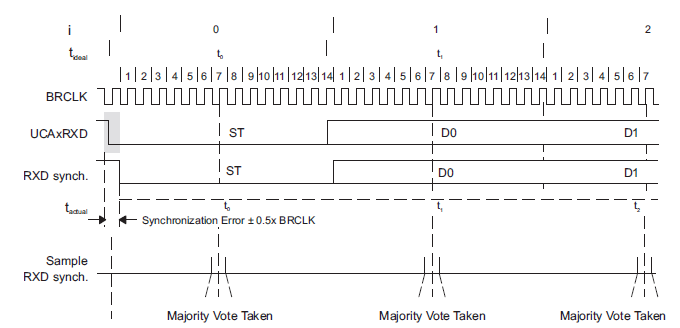
MSP430FR2311 User’s Guide中指出，接收端误差包括两部分：一个是从发射端start bit开始边沿到该边沿被接收端识别的误差，另一个是每个数据bit实际识别时刻和理想识别时刻的偏差。如图3所示。

图3 接收端两种误差
第一种误差用Tsync表示，Tsync = ±0.5BRCLK。
对于第二种误差，由于理想情况下接收端是在数据bit时长一半的位置进行采样识别，所以在进行误差计算时，是以该时刻为参考进行计算，而不像发射端，是以该数据bit理想时长结束的位置为参考进行计算。
MSP430FR2311 User’s Guide中给出了计算公式，但是这些公式中包含的元素太多不便理解。本文通过简化的方式来进行理解和计算，可以得到相同的累积误差结果。
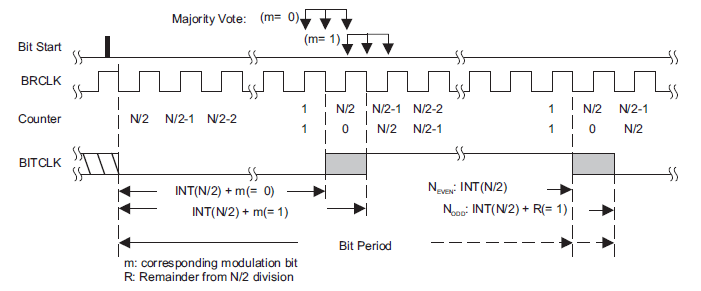
图4为MSP430FR2311的Majority Vote示意图，从图中可以看出Majority Vote在三个边沿的位置进行数据采样，采样的中心位置为INT(N/2)+m，其中N=INT(BRCLK/BITCLK), m为UCBRSx中对应于该数据bit的UCBRSx.m值。理想的数据bit采样中心位置为0.5/BITCLK。
图4 Majority Vote示意图
所以对于从Start bit开始的第i个数据bit，其采样中心位置时刻为Tsync，前i-1个数据bit实际总时长和该数据bit采样中心位置时长的总和，然后和理想的第i个数据bit采样中心位置时刻进行比较，便可得出第i个数据bit的累积误差。
以时钟源频率BRCLK 32768Hz，波特率BITCLK 2400Hz为例，32768/2400=13.6533，所以UCOS16=0，UCBRx=13，UCBRSx=0xB6.理想数据bit采样中心位置13.6533/2=6.8267BRCLK。
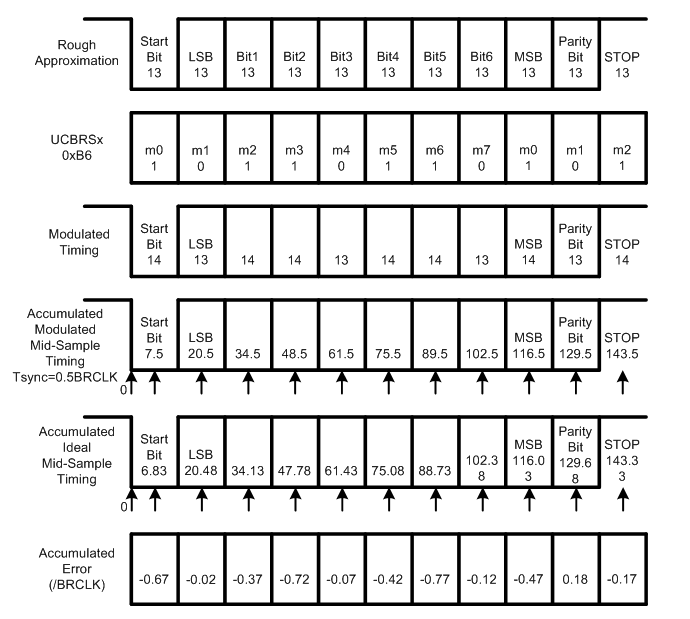
如图5和图6所示，在每个数据bit采样中心位置时刻，实际累积采样时刻和理想累积采样时刻存在误差。
当考虑Tsync=0.5BRCLK时，如图5所示。
对于Start bit，理想数据bit累积采样中心位置时刻为6.83BRCLK，实际数据bit累积采样中心位置时刻为7.5BRCLK，误差为6.83BRCLK-7.5BRCLK=-0.67BRCLK。
对于LSB bit，理想数据bit累积采样中心位置时刻为20.48BRCLK，实际数据bit累积采样中心位置时刻为20.5BRCLK，误差为20.48BRCLK-20.5BRCLK=-0.02BRCLK。
对于Bit1，理想数据bit累积采样中心位置时刻为34.13BRCLK，实际数据bit累积采样中心位置时刻为34.5BRCLK，误差为34.13BRCLK-34.5BRCLK=-0.37BRCLK。
后续bit位的累积误差以此类推。
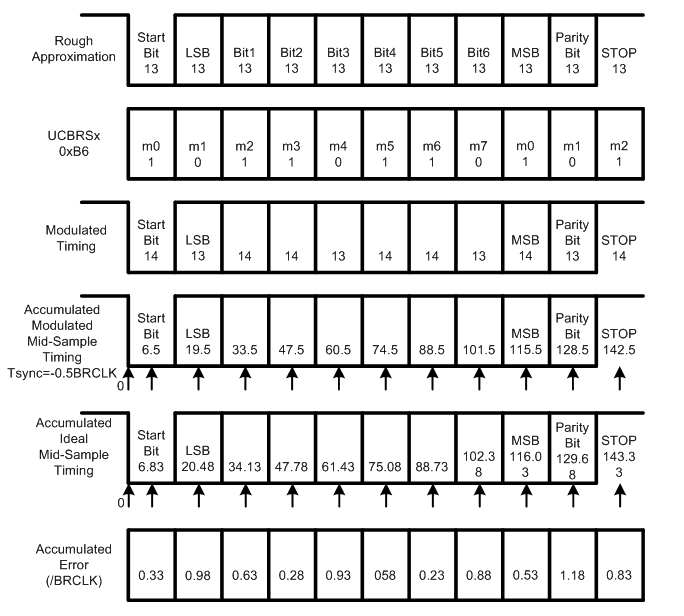
当考虑Tsync=-0.5BRCLK时，如图6所示。
分析方法和图5一样，不再赘述。
图5低频波特率的接收端累积误差示意图，Tsync=0.5BRCLK

图6低频波特率的接收端累积误差示意图，Tsync=-0.5BRCLK
以下是低频波特率的接收端累积误差的公式推导。
t_bits_ideal_RX为接收端理想数据bit累积采样中心位置时刻。
t_bits_ideal_RX = (i+0.5)/BITCLK                                                                                                                      (11)
t_bit_period_RX为接收端实际数据bit采样中心位置时刻。每个数据bit采样中心位置时刻的BRCLK个数等于INT(0.5UCBRx)和UCBRSx的对应调制值UCBRSx.m之和。
t_bit_period_RX = [INT(0.5*UCBRx) +UCBRSx.m]/BRCLK                                                                               (12)
t_bits_before_RX为当前数据bit之前的所有i-1个数据bit实际累积数据时长。
t_bits_before_RX[0] = 0
t_bits_before_RX = t_bits_before_RX[i-1] + (UCBRx[i-1] + UCBRSx.m[i-1])/BRCLK, 其中i≠0                (13)
其中t_bits_before_RX[i-1]为所有i-2个数据bit实际累积数据时长，(UCBRx[i-1] + UCBRSx.m[i-1])/BRCLK为第i-1个数据bit实际数据时长。
t_bits_RX为接收端实际数据bit累积采样中心位置时刻。
t_bits_TX = Tsync + t_bit_period_RX + t_bits_before_RX                                                                   (14)
定义Error_TX为接收端实际数据bit累积采样中心位置时刻相对于理想数据bit累积采样中心位置时刻的误差占理想数据bit时长的百分比，单位为%
Error_TX=( t_bits_ideal_TX- T_bits_TX)*BITCLK*100                                                                            (15)
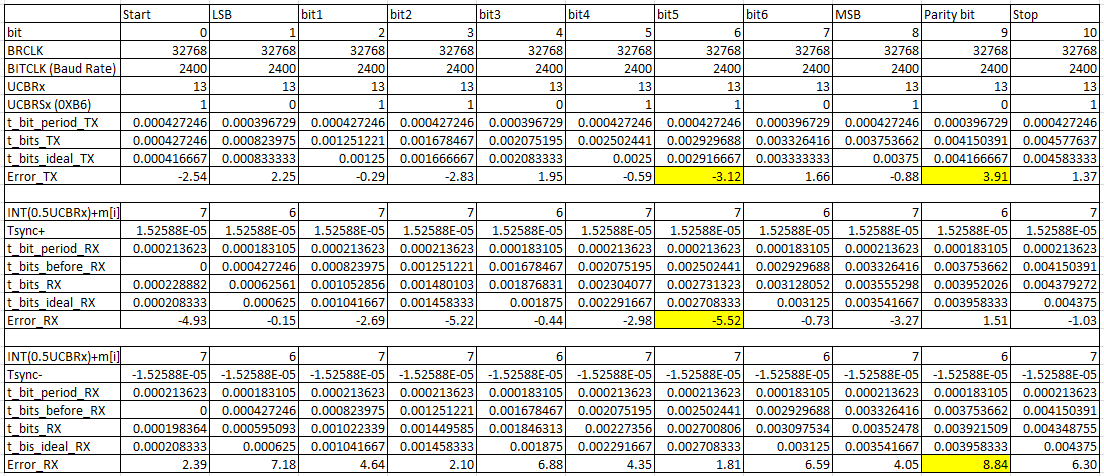
表3为带入例程中数据的Error_TX。
从表3中可以看到，最大正Error_TX为8.84%，最小负Error_TX为-5.52%.
表3 Error_TX

高频波特率的接收端累积误差
以时钟源频率BRCLK 4000000Hz，波特率BITCLK 57600为例，4000000/57600=69.4444，所以UCOS16=1，UCBRx=4，UCBRFx=5，UCBRSx=0x55. 理想数据bit采样中心位置69.4444/2=34.7222BRCLK.
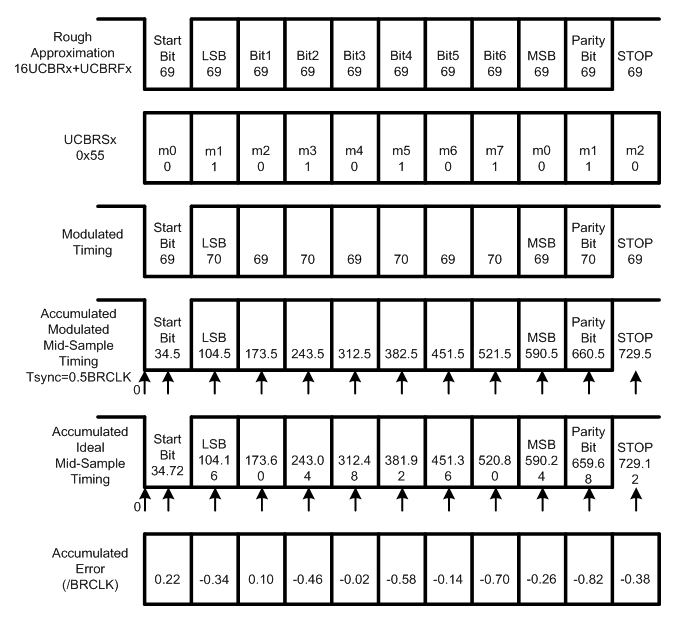
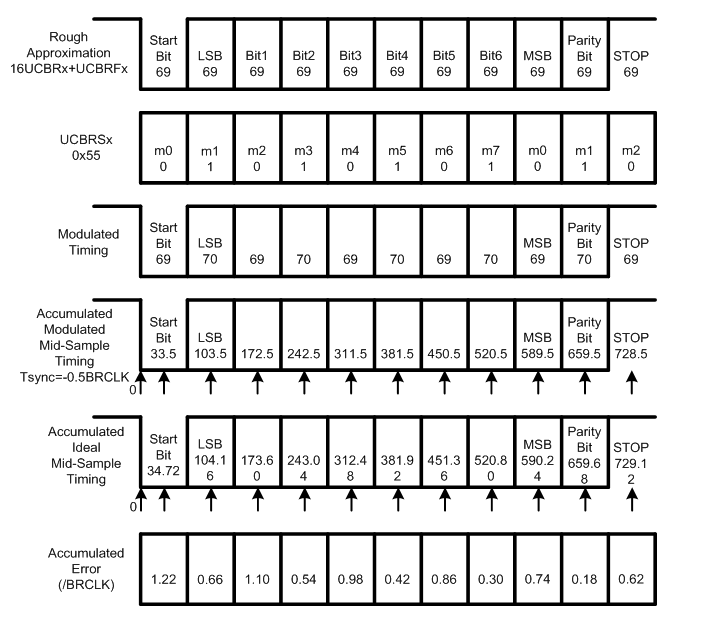
如图7和图8所示，在每个数据bit累积采样中心位置时刻，实际采样时刻和理想采样时刻存在误差。
当考虑Tsync=0.5BRCLK时，如图7所示。
对于Start bit，理想数据bit累积采样中心位置时刻为34.72BRCLK，实际数据bit累积采样中心位置时刻为34.5BRCLK，误差为34.72BRCLK-34.5BRCLK=0.22BRCLK。
对于LSB bit，理想数据bit累积采样中心位置时刻为104.16BRCLK，实际数据bit累积采样中心位置时刻为104.5BRCLK，误差为104.16BRCLK-104.5BRCLK=-0.34BRCLK。
对于Bit1，理想数据bit累积采样中心位置时刻为173.60，实际数据bit累积采样中心位置时刻为173.5BRCLK，误差为173.60BRCLK-173.5BRCLK=0.10BRCLK。
后续bit位的累积误差以此类推。
当考虑Tsync=-0.5BRCLK时，如图8所示。
分析方法和图7一样，不再赘述。

图7高频波特率的接收端累积误差示意图，Tsync=0.5BRCLK

图8高频波特率的接收端累积误差示意图，Tsync=-0.5BRCLK
以下是高频波特率的接收端累积误差的公式推导。
t_bits_ideal_RX为接收端理想数据bit累积采样中心位置时刻。
t_bits_ideal_RX = (i+0.5)/BITCLK                                                                                                                      (16)
t_bit_period_RX为接收端实际数据bit采样中心位置时刻。每个数据bit采样中心位置时刻的BRCLK个数等于INT[0.5*(16*UCBRx+UCBRFx)]和UCBRSx的对应调制值UCBRSx.m之和。
t_bit_period_RX = [INT(0.5*(16*UCBRx+UCBRFx)) +UCBRSx.m]/BRCLK                                                    (17)
t_bits_before_RX为当前数据bit之前的所有i-1个数据bit实际累积数据时长。
t_bits_before_RX[0] = 0
t_bits_before_RX = t_bits_before_RX[i-1] + (16*UCBRx+UCBRFx + UCBRSx.m)/BRCLK, 其中i≠0       (18)
其中t_bits_before_RX[i-1]为所有i-2个数据bit实际累积数据时长，(16*UCBRx+UCBRFx + UCBRSx.m)/BRCLK为第i-1个数据bit实际数据时长。
t_bits_RX为接收端实际数据bit累积采样中心位置时刻。
t_bits_TX = Tsync + t_bit_period_RX + t_bits_before_RX                                                                   (19)
定义Error_TX为接收端实际数据bit累积采样中心位置时刻相对于理想数据bit累积采样中心位置时刻的误差占理想数据bit时长的百分比，单位为%
Error_TX=( t_bits_ideal_TX- T_bits_TX)*BITCLK*100                                                                            (20)
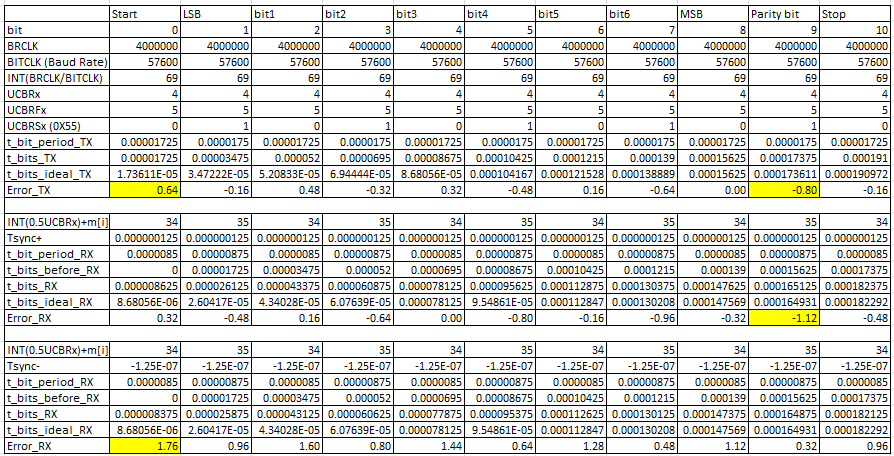
表4为带入例程中数据的Error_TX。
从表4中可以看到，最大正Error_TX为1.76%，最小负Error_TX为-1.12%.
表4 Error_TX

时钟源频率优选
时钟源频率优选需要考虑两方面的因素：
尽量降低发射端累积误差和接收端累积误差
对于Majority Vote架构，过高的时钟源频率会减小Majority Vote的检测窗口，降低Majority Vote的性能

以波特率9600Hz为例, Error_TX和Error_RX如表5所示，根据时钟源优选原则，选择1000000Hz。
表5 Error_TX和Error_RX
BRCLK
BITCLK
Error_TX+ (%)
Error_TX- (%)
Error_RX+ (%)
Error_RX- (%)
32768
9600
16.02
-17.19
37.30
-23.24
1000000
9600
0.64
-0.48
1.04
-1.04
8000000
9600
0.04
-0.08
0.14
-0.10

回复评论

暂无评论，赶紧抢沙发吧

BRCLK	BITCLK	Error_TX+ (%)	Error_TX- (%)	Error_RX+ (%)	Error_RX- (%)
32768	9600	16.02	-17.19	37.30	-23.24
1000000	9600	0.64	-0.48	1.04	-1.04
8000000	9600	0.04	-0.08	0.14	-0.10