本文主要是收拾战略迭代的部分,重在阐明原理。李宏毅的视频,见网上。
终究阐明OpenAI的默认强化学习算法PPO的部分。(Proximal Policy Optimization)
蓝色标记为有待查阅具体代码。不同于强化学习的值迭代的简单了解和表达,战略迭代更需要耐性、仔细、考虑。

战略 𝜋 是能够用,带着练习参数𝜃的神经网络表明。战略𝜋网络,输入当时调查值observation(state),输出action的概率。
该网络的输出action,如果是接连的,每个动效果一个神经元表明,大小能够为接连值。动作是离散行为,则每个神经元输出一个概率。该概率表明为,该行为或许采取的或许性。在实际行为进程中,从该概率中进行采样。
下图,当输入状况S,则输出的三个离散动作的概率。
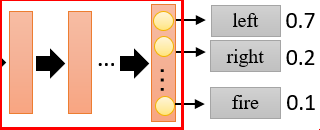
强化学习中,Agent的方针是,在MDP(马尔科夫决策进程)模型中,最大化累积奖赏R。如下:在每一幕的运行进程中,最大化累积奖赏R,为一切r的和。
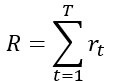
在一条马尔科夫链中,其每一条轨道的表达运用 𝜏 表明。𝑝_𝜃 (𝜏)表明为该条轨道 𝜏 呈现的概率。𝑝(𝑠_1 )为初始时,呈现𝑠_1的概率。𝑝_𝜃 (𝑎_1 |𝑠_1 )等,为在𝑠_1下挑选𝑎_1的概率。之后的𝑝(𝑠_2 |𝑠_1,𝑎_1 )等类似,表明在𝑠_1,𝑎_1下,能到达𝑠_2的概率(搬运概率)。
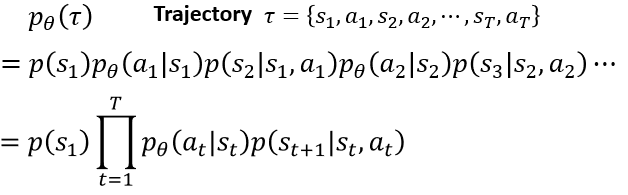
在每个轨道 𝜏 中,每一对s与a,发生一个奖赏r。终究,在每一个轨道中,发生一个累积奖赏R。
针对同一个战略模型 𝜋 ,其每次交互的环境、每次的行为等,都是不确定的,终究有不同的轨道 𝜏 。
可是,轨道都是由该战略模型 𝜋 得到的,并得到不同的累积奖赏R。强化学习的优化方针,则是优化该模型,使得均匀累积(希望奖赏)奖赏最大化。
如下的表达中,均匀奖赏(奖赏希望)为,在每条轨道 下发生的累积奖赏,和该轨道发生的概率𝑝_𝜃 (𝜏),的乘积和。
运用希望的表达中,为,在概率𝑝_𝜃 (𝜏)下,采样轨道 𝜏 ,在一切轨道 𝜏 下的,均匀奖赏R。
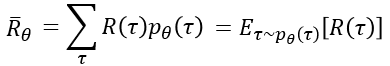

优化方针为奖赏希望,使得其最大化,则直接经过求梯度方法,对其求梯度,运用梯度上升的方法,得到最大化希望奖赏。
实质上,对奖赏R求梯度,作为自变量的为𝜃。𝜃为战略模型 𝜋 的参数(神经网络的权值、练习参数),实质上也便是,经过练习模型 𝜋 ,终究取得最大的希望奖赏R。
经过蓝色方框的公式调用,得到第二行,经过希望的表明改换,得到第三行左。
在执行足够多的N次轨道后,首先,该N个轨道,仍然是由战略 𝜋 中的𝜃决议的。在足够多的N下,根本服从希望下标𝜏~𝑝_𝜃 (𝜏)中的轨道散布,所以能够约等。
第四行对第三行右,进行了进一步推导,将𝑝_𝜃的时间线进行了打开。可是是不是少了一个搬运概率。
不过很明显的是,搬运概率在轨道中,是由环境Environment确定的,因而运用𝜃作为自变量求梯度,其为常数表明,不影响终究梯度方向。
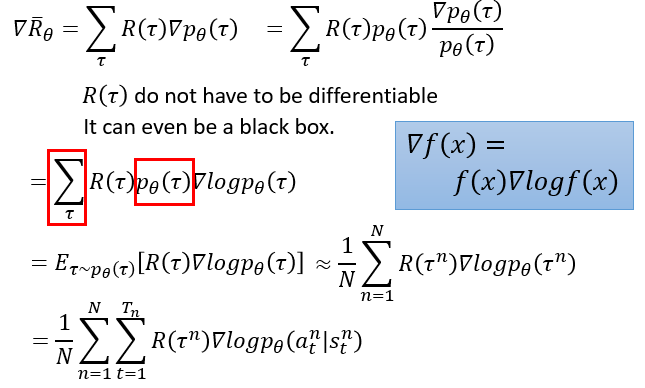
因而,战略梯度的练习表明如下:其间的梯度在上图中现已得到核算。
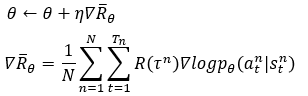
在实际完成进程中,如运用TensorFlow核算梯度,其核算进程能够和交叉熵有关。
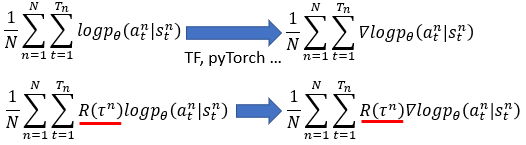

战略梯度的核算流程上:
1 依据Agent和环境的交互,经过战略模型 𝜋 得到一条轨道𝜏 。在该轨道完毕后,得到累积奖赏R。
2 运用梯度上升的方法,最大化R。在梯度上升的核算进程中,𝑙𝑜𝑔𝑝_𝜃其实便是战略网络 𝜋 输出的概率,实质上也便是梯度上升,改动 𝜋,然后最大化R。
重复以上进程,使得R越来越大即可。
战略梯度在运用进程中发现有两个问题:
1 在一些强化学习环境中,轨道𝜏下的一切行为奖赏,都是正的奖赏值,则依据公式,每次都是梯度上升。
那么,使得R最大化的进程中,即,战略网络 𝜋 被练习时,rar破解器采样的影响导致,针对同一个状况observation(state)时,输出的行为概率散布更倾向于采样更多的地方练习。
在同一状况下,abc三个行为的概率和为1,抱负状况是b的动作最优。可是a采样次数更多而b更少,则依据梯度上升时R都是大于0,战略网络对a的行为强度增强,导致了相对于b行为的强度削减。同理图中第二行,当a没有被采样一定数量多,则a会相对于抱负状况下削减。
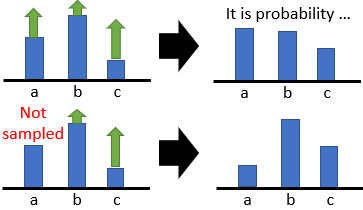
因而运用进程中,对R添加baseline,使得R能够呈现负值,只添加哪些高于均匀奖赏的R对应的轨道战略。呈现了负值,则表明该轨道不够优秀,应该下降,采样越多,则下降越多。
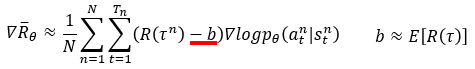
2 奖赏R的衡量问题。在战略网络 𝜋 下,整条轨道的累积奖赏R,不足以衡量 𝜋 中每一个输出行为概率的好坏。每个输出应该对应到每个奖赏,而不是整条轨道R。
在轨道中,当时行为a,在一定程度上决议了,后边的状况-行为对,越往后的状况行为对,其决议性的影响越小。因而,当时行为a的奖赏r,为该行为和之后一切行为的和。并运用𝛾衰减因子,模仿其决议性影响越小导致的本次行为a的奖赏越小。


重要性采样表明为:无法得知f(x)在p散布上的希望,则运用恣意的散布q,来间接得到f(x)在p散布上的希望。
具体操作如第二行,终究:f(x)在p散布上的希望,转化为了f(x)*p(x)/q(x)在散布q上的希望。
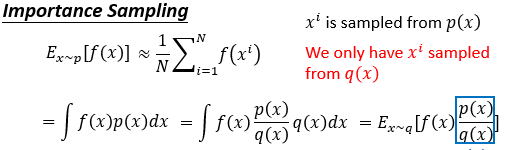
尽管希望持平,可是方差是不等的。下图中,榜首行为重要性采样,第三行为方差打开为希望形式,第四行前者又运用了一次重要性采样,后者直接代换。
结论是,重要性采样前后运用的未知散布p和已知散布q,若比值为1(完全相同),则方差也相同。比值越偏,方差越偏。
方差越偏导致的问题是,zip破解当采样次数不够多,则导致重要性采样定理的前后希望值的偏差,呈现的或许性越大。
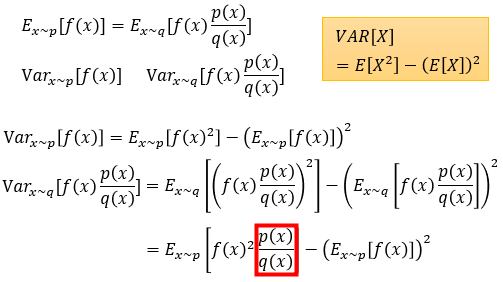
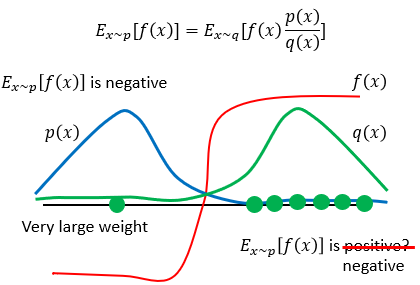
运用如下所述,前者在p散布上的希望,f(x)*p(x)的累加和,根本为负值。后者,当采样点过少时,由于q(x)集中在f(x)的正值部分,尽管p(x)*f(x)/q(x)也很小,可是其值为正。只有采样到一个别的的点,p(x)*f(x)/q(x)又对应了很大,才导致了希望为负。才使得重要性采样定理的前后希望一致性。

on-policy,其进程和上述战略梯度相同:战略模型𝜋 和环境交互取得轨道,然后运用该轨道进行练习。重复该进程。
off-policy,其战略模型𝜋' 和环境交互得到轨道,战略模型𝜋 学习该轨道,而战略模型𝜋 自身没有和环境进行交互。
在线战略中,其学习完的轨道,直接丢掉不能再学习了,由于模型𝜋学习了自身的轨道今后,模型有了改变,之前的轨道不再是由该变更过的模型𝜋发生。
离线战略中,其运用别的的模型𝜋',取得的多条轨道,用于战略模型𝜋的学习,学习完今后的轨道,由于𝜋'没有改动,其生成的轨道仍然可用。
(以为是学习的方针,本应该是一个固定的散布,而不是一个变来变去的散布)相对于在线战略,离线战略效率,由于轨道的生成和学习进程的方便性,而变得更高。
𝜃′对应于模型𝜋',运用重要性采样定理,将在线战略转化为离线战略:
其间榜首行为在线战略(之前的战略梯度的大致表现形式,从𝜋中取得轨道),第二行运用𝜋'中采样,取得轨道,核算梯度。
在多次采样后,二者的梯度应该持平的。
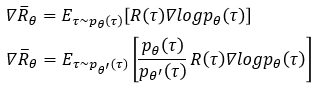
如下是战略梯度的具体表明形式,并运用重要性采样定理进行的改换。榜首行为在线战略,第二行变为离线战略,由于离线战略的奖赏部分A,为𝜋'所发生,则变为了𝐴^(𝜃′ )。变了今后和之前的式子,还能持平吗,不能吧,假设能够,持续推导
第三行中,𝑃_𝜃 (𝑠_𝑡,𝑎_𝑡 )表明的是𝑠_𝑡,𝑎_𝑡呈现的概率,经过概率逻辑,改换为两项。而后项的上下两个就权且以为持平了,比值为1。其实应该是不等的。可是不易求得,并以为持平。
最终一行,经过图中的蓝色框公式,反推得到的f(x),即离线战略下rar破解的优化方针函数J(其实和原始状况下的方针函数R的希望类似吧)。


TRPO (Trust Region Policy Optimization)算法是先于Proximal Policy Optimization (PPO)算法提出的。
在TRPO中,其实运用的方法便是在线转离线的战略了,并额定要求𝜃,𝜃′有一个类似性(KL散度,数据的原始散布和近似散布之间的类似性)
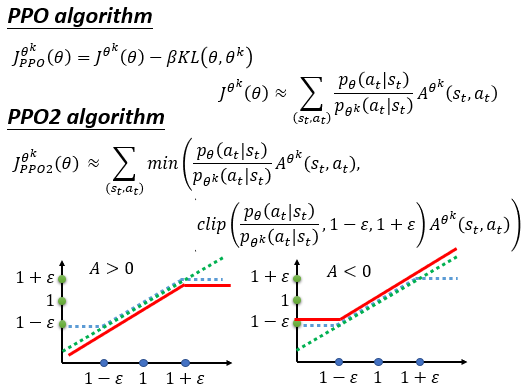
在PPO中,将类似性写入了优化方针中。要求优化方针尽或许的大,则KL散度尽或许小。

KL散度过小,则𝜋'和𝜋之间的类似度高,或许学不到什么吧?类似度过低,则由于重要性采样的问题,方差影响加之采样量不足,使得前后等式不成立。
这儿的𝜃^𝑘表明有多个𝜋',用于生成轨道。

比照PPO2,其实质仍然是控制𝜃,𝜃′的类似性。可是没有运用KL散度,而是运用clip方法,限制两者的比值在一个范围内。使妥当A大于0增强该战略,或者A<0限制该战略的强度,都在一个范围内。
Le vent se lève! . . . il faut tenter de vivre!
Le vent se lève! . . . il faut tenter de vivre!
本文转载于:https://blog.csdn.net/dafengit/article/details/106073709转载请标明出处
