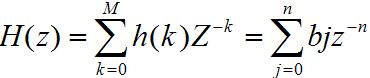数字滤波器最为常用的就是线性时不变LTI(Linear Time Invariant)滤波器,LTI与其输入信号相互作用,经过一个称为线性卷积的过程。LTI数字滤波器通常可以分为有限脉冲响应FIR(Finite Impulse Respones)和无限脉冲响应IIR(Infinite Impulse Response)两大类。其中,FIR滤波器由有限个采样值将卷积的数量降低到在每个采样时刻为有限个,而IIR滤波器需要执行无限数量次卷积。
数字滤波器公式中常用的符号:
FIR 数字滤波器设计原理:
有限冲击响应(FIR)滤波器的基本结构如是一个分节的延时线,把每一节的输出加权累加,得到滤波器的输出。数学上表示为:
其结构如下图:
它由用一条均匀间隔抽头的延迟线对抽头信号进行加权求和构成。
例如,三阶FIR的数字滤波器可以表示为:
y(n)=h0x(n)+h1x(n-1)+h2x(n-2)+h3x(n-3),其低通特性跟系数h0,h1,h3有关。
FIR数字滤波器的系统函数可以表示为:
从上公式可以看出,其系统函数就是Z^-1的多项式,其设计就是一个数学逼近问题,即用一个因果稳定的系统函数去逼近给定的性能要求,以确定滤波器的系数。
上面这部简单介绍了FIR 直接实现型结构的 DF(Digtial Filter).FIR 还有多种实现结构,例如:
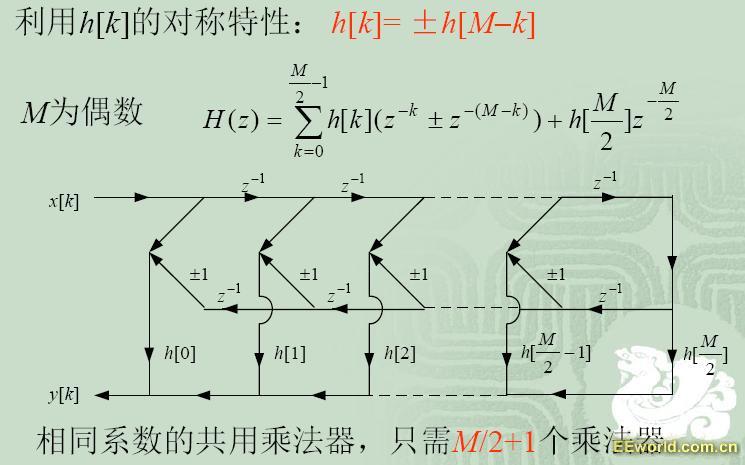
线性相位FIR DF结构:
上面图示M为偶数,FIR系统函数和输出图示表示法。
M位奇数表示法如下:
其实FIR还有其他模型结构,例如频率取样型结构,级联型结构等等各类结构,但在数字编程中,比如在DSP或FPGA中实现FIR,通常常用的直接型理想结构。因此本例中重点讨论直接型FIR。
哪究竟FIR 滤波设计,需要哪些步骤和方法?
基本步骤如下:
数字滤波器根据其冲激响应函数的时域特性,可分为2种,即无限长冲激响应(IIR)滤波器和有限长冲激响应(FIR)滤波器。FIR系统不像IIR系统那样易取得较好的通带和阻带衰减特性,要取得较好的衰减特性,一般要求H(z)阶次要高,也即M要大。FIR系统有自己突出的优点:系统总是稳定的;易实现线性相位;允许设计多通带(或多阻带)滤波器,后两项都是IIR系统不易实现的。FIR数字滤波器的设计方法有多种,如窗函数设计法、频率采样法和Chebyshev逼近法等。随着Matlab软件尤其是Matlab的信号处理工作箱的不断完善,不仅数字滤波器的计算机辅助设计有了可能,而且还可以使设计达到最优化。
(1)确定技术指标
在设计一个滤波器之前,必须首先根据工程实际的需要确定滤波器的技术指标。在很多实际应用中,数字滤波器常被用来实现选频操作。因此,指标的形式一般在频域中给出幅度和相位响应。幅度指标主要以2种方式给出。第一种是绝对指标。他提供对幅度响应函数的要求,一般应用于FIR滤波器的设计。第二种指标是相对指标。他以分贝值的形式给出要求。本文中滤波器的设计就以线性相位FIR滤波器的设计为例。
(2)逼近
确定了技术指标后,就可以建立一个目标的数字滤波器模型(通常采用理想的数字滤波器模型)。之后,利用数字滤波器的设计方法(窗函数法、频率采样法等),设计出一个实际滤波器模型来逼近给定的目标。
(3)性能分析和计算机仿真
上两步的结果是得到以差分或系统函数或冲激响应描述的滤波器。根据这个描述就可以分析其频率特性和相位特性,以验证设计结果是否满足指标要求;或者利用计算机仿真实现设计的滤波器,再分析滤波结果来判断。